L'expérience de la gomme quantique à choix retardé...

L’ extraordinaire expérience de la gomme quantique à choix retardé est une expérience de physique quantique qui prolonge celles  de Thomas Young*  (1801) et aussi celle d'Alain Aspect (1980) en y introduisant ce qui semble être une rétroaction dans le temps.
Elle fut proposée en 1982 par Marlan Scully et Kai Drühl.


Pour mémoire "l'expérience des fentes de Young" illustre la dualité onde-particule : les interférences montrent que la matière ( photons, électrons, neutrons, atomes, molécules,) présente un comportement ondulatoire, mais la façon dont elles sont détectées (impact sur un écran) montre leur comportement de particules (discontinues).


1/ Pour bien saisir, il faut d' abord se remémorer cette variante "aux miroirs" de l'expérience des fentes de Young :

Le photon émis a 1 chance sur 2 de traverser A (pour aller par B, en I)  et 1 sur 2 de se réfléchir en A (pour aller par C en I).

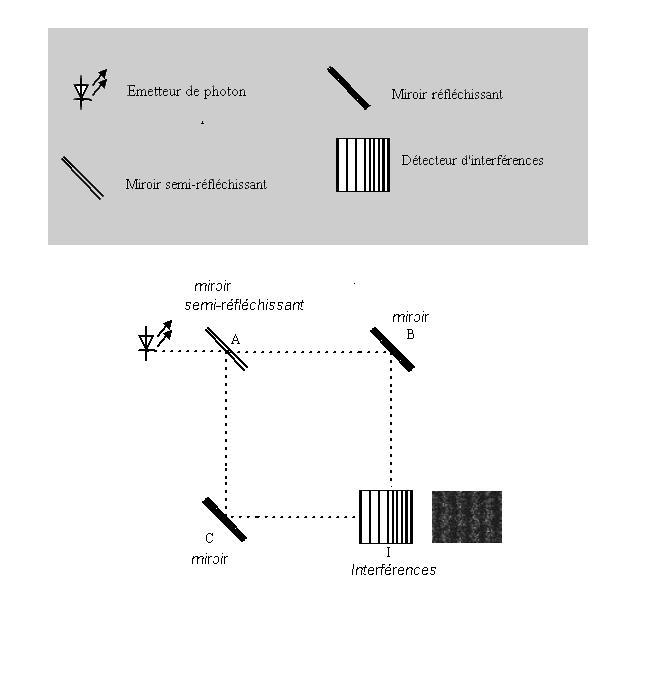
On ne sait pas quel chemin il a pris dans ce cas , et on observe une figure d'interférence en I. C'est à dire qu'il s'est comporté comme une onde.

Jusque là tout va bien.

2/ Si on ajoute des détecteurs de photons à ce schéma d'expérience pour savoir quel chemin a pris le photon:

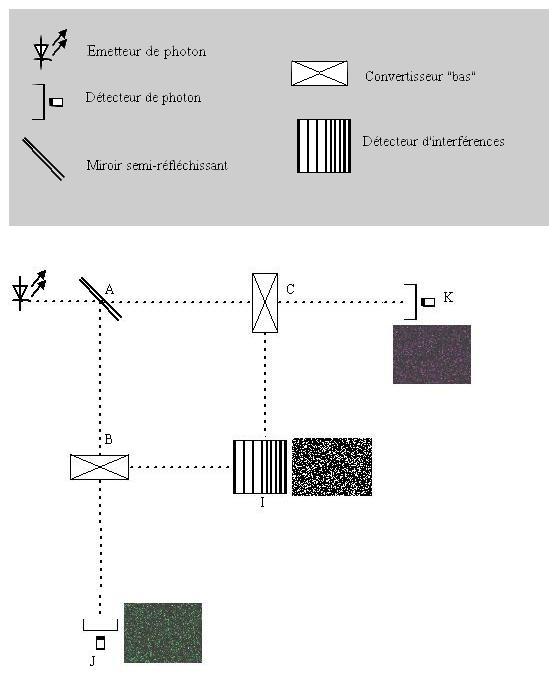
Le fait d'ajouter des détecteurs (on sait s' il est passé par B ou par C) fait effondrer l'état quantique, il n'y a plus d'onde, plus d'interférence.

Le convertisseur bas est un appareil qui, à partir d'un "photon en entrée", crée deux "photons en sortie", intriqués, (et de longueur d'onde double par rapport au photon en entrée). Ces convertisseurs ne détruisent pas l'état quantique du photon, car ils ne font  pas de "mesure".

Plus précisément 1 des deux "photons de sortie" est détecté, l'autre pas, mais comme ils sont intriqués, on sait par où est passé le "photon d'entrée".

C'est là qu'intervient la redoutable habileté de cette expérience ...

3/  On ajoute des miroirs semi-réfléchissants en E et D devant les détecteurs  K et J. Le photon 1 fois sur 2 traverse et se fait détecter. Une fois sur 2 il est redirigé par réflexion vers F, quatrième miroir semi-réfléchissant du montage, la clef de ce gommage quantique.

Qu'il vienne de E ou de B, le photon en F traversera 1 fois sur 2, et sera réfléchi 1 fois sur 2. De ce fait, les deux détecteurs H et G, détecteront des photons venus indifféremment de E ou de D sans que l'on puisse le préciser. Le miroir semi-réfléchissant F , imaginé par Scully  est la gomme quantique: il détruit l'information permettant de savoir par quel chemin est passé le photon.

Il est crucial de noter que les photons qui percutent la plaque photographique en I, le font AVANT que leur jumeau intriqué ne parvienne soit en J/K, soit en G/H.

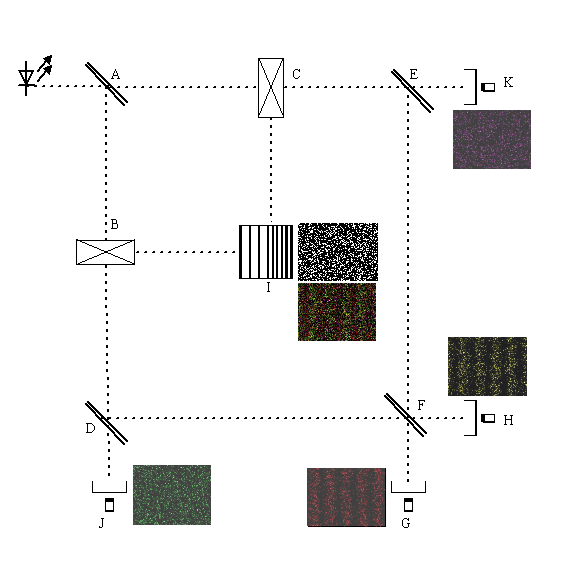
Constatations:

-Une moitié des photons arrivent en K ou J, (chemin connu par la détection) et on vérifie qu'ils n'ont pas donné d'interférence en I. L'autre moitié arrive en G ou H (sans que l'on connaisse leur chemin malgré la détection)  et on voit qu'ils ont produit une figure d'interférence en I.

-Le résultat enregistré en I est  fixé AVANT que le photon témoin n'ait été détecté en J/K (chemin connu, pas d'interférence) ou en G/H (chemin indéterminé , interférence).

Comment le photon atteignant I peut-il savoir que son jumeau intriqué sera détecté plus tard en J/K ou non ?

Telle est la question essentielle de cette expérience.

Il semble se comporter irréversiblement, à un instant précis (en I), en fonction de ce qui sera déterminé par hasard un certain temps plus tard (en G/H ou J/k), donc dans le futur,.



***

Page Wiki sur cette expérience.



Une nouvelle version de cette expérience a été réalisée en utilisant des satellites dans l'espace, sur lesquels des photons issus d'un laser ont rebondi.

La distance qu'ils ont parcourue dans l'expérience est de l'ordre de 3.500 km et pourtant, les résultats obtenus sont toujours conformes aux prédictions de la mécanique quantique.

***

* Pour se remémorer l'expérience des fentes de Young.



blog source
 
Appendice:
Exemple: interférences à la surface de l'eau